- その1 - 説明、ソースコード
- その2 - Q.1 〜 Q.106
- その3 - Q.107 〜 Q.206
- その4 - Q.207 〜 Q.366
- その5 - Q.367 〜 Q.514
- その7 - Q.515 〜 Q.700
- その8 - Q.701 〜 Q.999
- その9 - Q.1000 〜 Q.1119
今回は数学的な話が入っているので、そういうのが嫌いなひとはそのまま その7 へ。
作ったプログラムの話
せっかく作ったので、どういう特性があるのか調べてみた。結論から言うと、ヒープソートが2分木を使うのはシンプルだからという単純な理由ではなかったという話です。
まず、このプログラムに関する話の前にヒープソートの性能について書くと、
- 最悪:
- 最良:
- 平均:
ということです(Wikipediaより抜粋)
プログラムでは、質問するとき必ず1がヒープ木の親、2以降は子になっています。また、若い番号の子の方が深い(世代が多い)です。従って、
1と答え続けると質問数の最小が得られます。2と答え続けると質問数の最大が得られます。- ランダムに回答するとほぼ平均が得られます。
の場合で、木の分岐数を増やしていくと、こんな感じ。
- Min: 質問される回数の最小値(最良ケース)
- Max: 質問される回数の最大値(最悪ケース)
- Ave: 平均(10回試行)
| M+1 | Min | Max | Ave | Min*M | Max*M | Ave*M |
|---|---|---|---|---|---|---|
| 3 | 1078 | 6174 | 2507.0 | 2154 | 12335 | 5010.3 |
| 4 | 958 | 4131 | 2422.7 | 2870 | 12374 | 7258.5 |
| 5 | 898 | 3382 | 2209.2 | 3585 | 13497 | 8818.7 |
| 6 | 862 | 2862 | 2068.2 | 4299 | 14269 | 10305.4 |
| 7 | 838 | 2711 | 1925.8 | 5012 | 16205 | 11511.5 |
| 8 | 821 | 2531 | 1841.0 | 5724 | 17631 | 12829.7 |
| 9 | 808 | 2313 | 1733.7 | 6435 | 18390 | 13798.2 |
| 10 | 798 | 2145 | 1641.0 | 7145 | 19196 | 14671.6 |
| 20 | 756 | 1796 | 1271.8 | 14190 | 33608 | 23826.2 |
| 30 | 743 | 1433 | 1029.7 | 21135 | 40739 | 29071.2 |
| 40 | 737 | 1417 | 896.6 | 27980 | 53759 | 33891.0 |
| 50 | 733 | 1403 | 827.7 | 34725 | 66379 | 39032.5 |
| 60 | 731 | 1391 | 801.9 | 41370 | 78599 | 45211.7 |
| 70 | 729 | 1379 | 774.6 | 47915 | 90419 | 50726.3 |
| 80 | 728 | 1368 | 764.6 | 54360 | 101839 | 56936.7 |
| 90 | 727 | 1357 | 757.3 | 60705 | 112859 | 63093.0 |
| 100 | 726 | 1346 | 750.4 | 66950 | 123479 | 68982.8 |
| 200 | 722 | 1242 | 727.1 | 123900 | 207679 | 124614.8 |
| 300 | 721 | 1141 | 723.1 | 170850 | 251879 | 171188.2 |
| 400 | 720 | 1040 | 720.7 | 207800 | 259160 | 207905.1 |
| 500 | 720 | 940 | 720.4 | 234750 | 259060 | 234788.7 |
| 600 | 720 | 840 | 720.2 | 251700 | 258960 | 251704.2 |
| 700 | 720 | 740 | 720.0 | 258650 | 258860 | 258650.0 |
分岐数を増やせば質問の回数は減る。ただ、実際に質問されればわかるが、大量の選択肢の中から目的のものを見つけるのに時間がかかってしまうわけで。それを考慮したものが、右側の3つ。これらは、左の列の値を 倍したもので、プログラムで最大もしくは最小を求めようとした時にかかる比較数が加味されることになります。
やはりそうなると、プログラムで比較してソートするなら2分木でやるのが効率的なんですね…。
M+1 が 3 で木は2分木となるわけだが、3つのうちの最大値をとる、ということで、少し非効率になっているので、実際のヒープソートはこれよりも速いと思います。
グラフにするとこんな感じ。
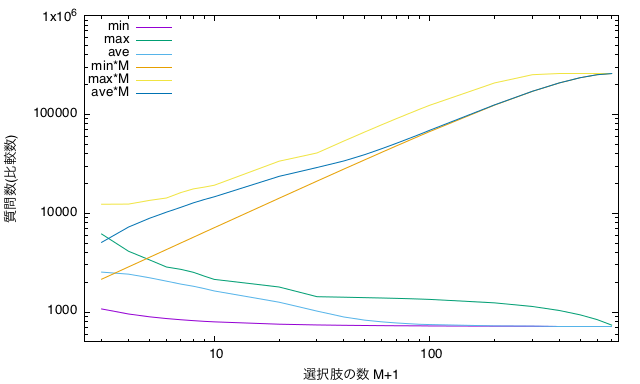
一応、 未満で最大値(最小値)が求められるなら多分木にする価値はあるのかもしれないけど、今のところ人間の頭以外では不可能なので…*1。
おまけ
前回、ツリーを見せようとして、画像のアップロードが失敗したくさくて載せなかったんだけど、今日見たらなぜかあったので載せとく。その5 の開始時点のものです。ただ、画像が大きすぎるので、文字は読めませんrz

*1:並列化などは計算速度は速くなるが、計算回数は減らない